Create Time: 2nd April 2024
Title: "[[DAA-Assignment-1]]"
status: DONE
Author:
  - AllenYGY
tags:
  - DAA
  - Assignment
created: 2024-04-02T17:07
updated: 2024-04-08T13:35

DAA-Assignment-1

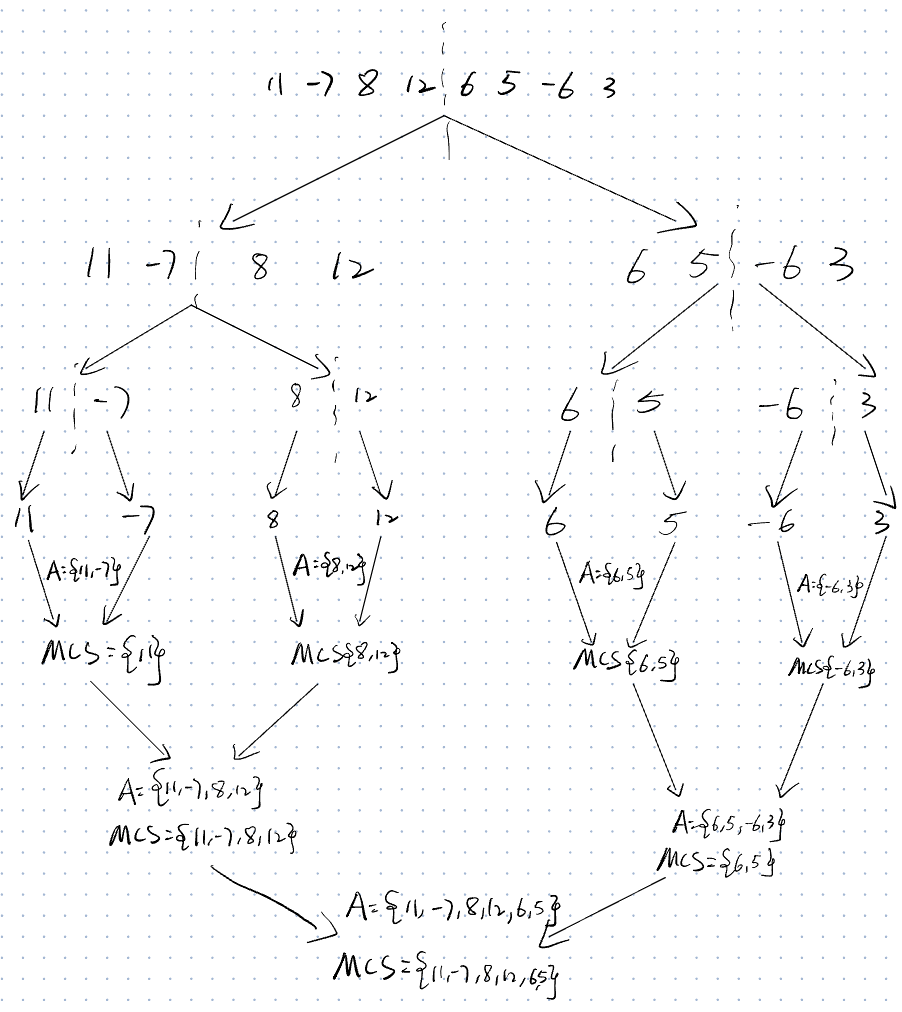
Question 1

Given the input A=[11, -7, 8, 12, 6, 5, -6, 3] , track the divide-and-conquer algorithm to find the maximum contiguous subarray. You need to show the recursive calls as a tree. The input and output for each recursive call should also be indicated as well.

Input: A=[11, -7, 8, 12, 6, 5, -6, 3]
Output: MCS of A

Algorithm Maximum Contiguous Subarray Problem

if $i = j$ then

return $R[i]$

else

$s1 \gets \text{MCS}(R, i, \lfloor(i+j)/2\rfloor)$ //Using floor function for lower rounding

$s2 \gets \text{MCS}(R, \lfloor(i+j)/2\rfloor + 1, j)$

$A \gets \text{MaxSuffix}(R, i, \lfloor(i+j)/2\rfloor) + \text{MaxPrefix}(R, \lfloor(i+j)/2\rfloor + 1, j)$

return $\text{MAX}(s1, s2, A)$

end if

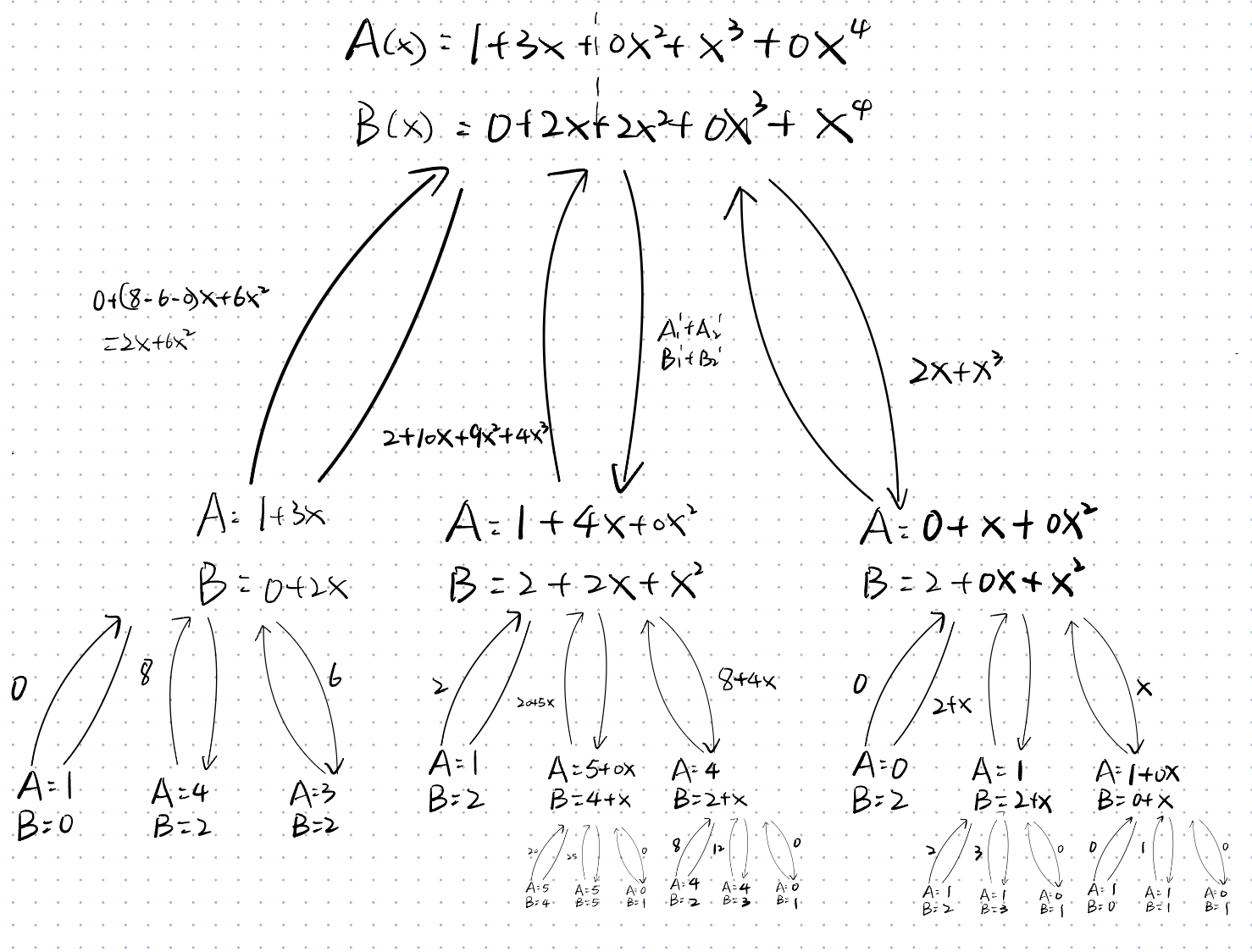
Question 2

Given two polynomials and , track the algorithm to calculate . You need to show the recursive calls as a tree. The input and output for each recursive call should also be indicated as well.

Input: Two polynomials A(X) and B(x) of order n
Output: The polynomial C(X) = A(x)B(x)

Algorithm Polynomial Multi2( $A(x),B(x)$ )

if $n=0$ then

return $a_0 \times b_0$

else

$A_0(x) = a_0 + a_1x + \dots + a_{\lfloor \frac{n}{2} \rfloor - 1}x^{\lfloor \frac{n}{2} \rfloor -1}$

$A_1(x) = a_{\lfloor \frac{n}{2} \rfloor} + a_{\lfloor \frac{n}{2} \rfloor +1}x + \dots + a_nx^{n-\lfloor \frac{n}{2} \rfloor}$

$B_0(x) = b_0 + b_1x + \dots + b_{\lfloor \frac{n}{2} \rfloor - 1}x^{\lfloor \frac{n}{2} \rfloor -1}$

$B_1(x) = b_{\lfloor \frac{n}{2} \rfloor} + b_{\lfloor \frac{n}{2} \rfloor +1}x + \dots + b_nx^{n-\lfloor \frac{n}{2} \rfloor}$

$Y(x) = \text{PolyMult2}(A_0(x)+A_1(x), B_0(x)+B_1(x))$

$U(x) = \text{PolyMult2}(A_0(x), B_0(x))$

$Z(x) = \text{PolyMult2}(A_1(x), B_1(x))$

return $U(x) + (Y(x) - U(x) - Z(x))x^{\lfloor \frac{n}{2} \rfloor} + Z(x)x^{2\lfloor \frac{n}{2} \rfloor}$

end if

Question 3

In the deterministic linear-time divide-and-conquer algorithm taught in class for the selection problem, the input array is divided into groups of 5 elements. Analyze the running time of the algorithm if the input array is divided into groups of 7. Does your algorithm run in linear time?

The Algorithm is still run in linear time

Algorithm Deterministic-Select( $A,p,r,i$ )

if $p=r$ then

return $A[p]$

end if

$q = Deterministic-Partition(A,p,r)$

$k = q - p + 1$

if $i = k$ then

return $A[q]$

end if

if $i < k$ then

return $Deterministic-Select(A,p,q-1,i)$

end if

if $i > k$ then

return $Deterministic-Select(A,q+1,r,i-k)$

end if

Assume always Deterministic-Select Right (wlog)

Proof Let if a is large enough;
By strong induction
Base case: When Assume for all Goal

Question 4

A segment is a pair of positive integers , where . Two segments and intersect if .

Given a sequence of of segments sorted increasingly by ’s ( if ) within the r ( for all ), design a divide-and-conquer algorithm to justify if there are two segments intersect.

Describe your algorithm in a high-level presentation.

Input:
- Segments a sequence of of segments sorted increasingly by ’s ( if ) within the r ( for all )
- Left to indicate left endpoint
- Right to indicate right endpoint
- R to indicate r ( for all )
Output:
- Boolean value indicating whether there is at least one pair of intersecting segments.

If the left and right indexes coincide, the intersect cannot be found. Return false;
Divide the array into two halves: the left sublist and the right sublist.
Recursively apply the algorithm to the left sublist to check for intersections.
Recursively apply the algorithm to the right sublist to check for intersections.
If any recursive call finds an intersection, return 'true' because we have already found the intersecting segments.
Otherwise look for MaxLeftB in the left sublist and MinRightA in the right list
If MinRightA is less than MaxLeftB, intersect is found
Otherwise return 'false'.

Write down the pseudo code.

Algorithm Check for Intersection in Segments

function DoesIntersect( $Segments$ , $Left$ , $Right$ , $R$ )

if $Left \geq Right$ then

return false

end if

$Mid \gets \lfloor(Left + Right) / 2\rfloor$

$LeftIntersect \gets$ DoesIntersect( $Segments$ , $Left$ , $Mid$ , $R$ )

$RightIntersect \gets$ DoesIntersect( $Segments$ , $Mid + 1$ , $Right$ , $R$ )

if $LeftIntersect$ or $RightIntersect$ then

return true

end if

$MaxLeftB \gets$ FindMaxB( $Segments$ , $Left$ , $Mid$ )

$MinRightA \gets$ FindMinA( $Segments$ , $Mid + 1$ , $Right$ )

if $MaxLeftB > MinRightA$ then

return true

end if

return false

end function

function FindMaxB( $Segments, Left, Mid$ )

$MaxB \gets -\infty$

for $i \gets Left$ to $Mid$ do

$MaxB \gets \max(MaxB, Segments[i].b)$

end for

return $MaxB$

end function

function FindMinA( $Segments, Mid, Right$ )

$MinA \gets \infty$

for $i \gets Mid + 1$ to $Right$ do

$MinA \gets \min(MinA, Segments[i].a)$

end for

return $MinA$

end function

Analyze the time complexity of your algorithm.

When
When

Question 5

Assume: The number of terms in the polynomials is always an integer power of

In other words, for some

Define a method to convert polynomials in general to polynomials whose number of terms is an integer power of 2.

If the number of terms of the polynomial is not a power of two
Then by adding the number of terms to the polynomial until the number of terms becomes a power of two, the coefficient of the added term is 0

Discuss the consequence by doing so. Does it increase the time complexity comparing to the original algorithm? Why?

Hint: please pay attention to the input size

Input: Two polynomials and of order
Output: The polynomials

Algorithm PolyMulti(A(x),B(x))

$A^{'}(x)=M(A(x))$

$B^{'}(x)=M(B(x))$

return GPolyMultic( $A^{'}(x),B^{'}(x)$ )

It will not increase the time complexity comparing to the original algorithm.
The time cost will slightly increase.
Suppose there are 2 polynomials with terms.
After the operation it now turn to terms.
In original algorithm the time complexity is
Now the time complexity is
There are almost the same time complexity