Create Time: 11th May 2024
Title: "[[DAA-Assignment-2]]"
status: DONE
Author:
  - AllenYGY
tags:
  - DAA
  - Assignment
created: 2024-05-11T13:58
updated: 2024-06-11T01:14

DAA-Assignment-2

Question 1

Question 2

Question 3

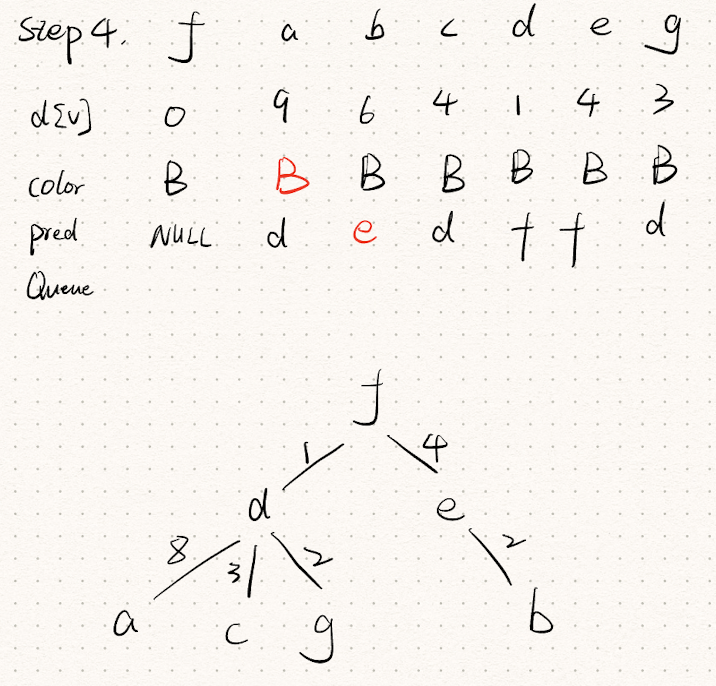
Question 4

A tree is the maximum spanning tree of a graph if is a spanning tree of and the weight on the tree is maximized.

Mr. Smart designs an algorithm to find the maximum spanning tree. Is his algorithm correct?

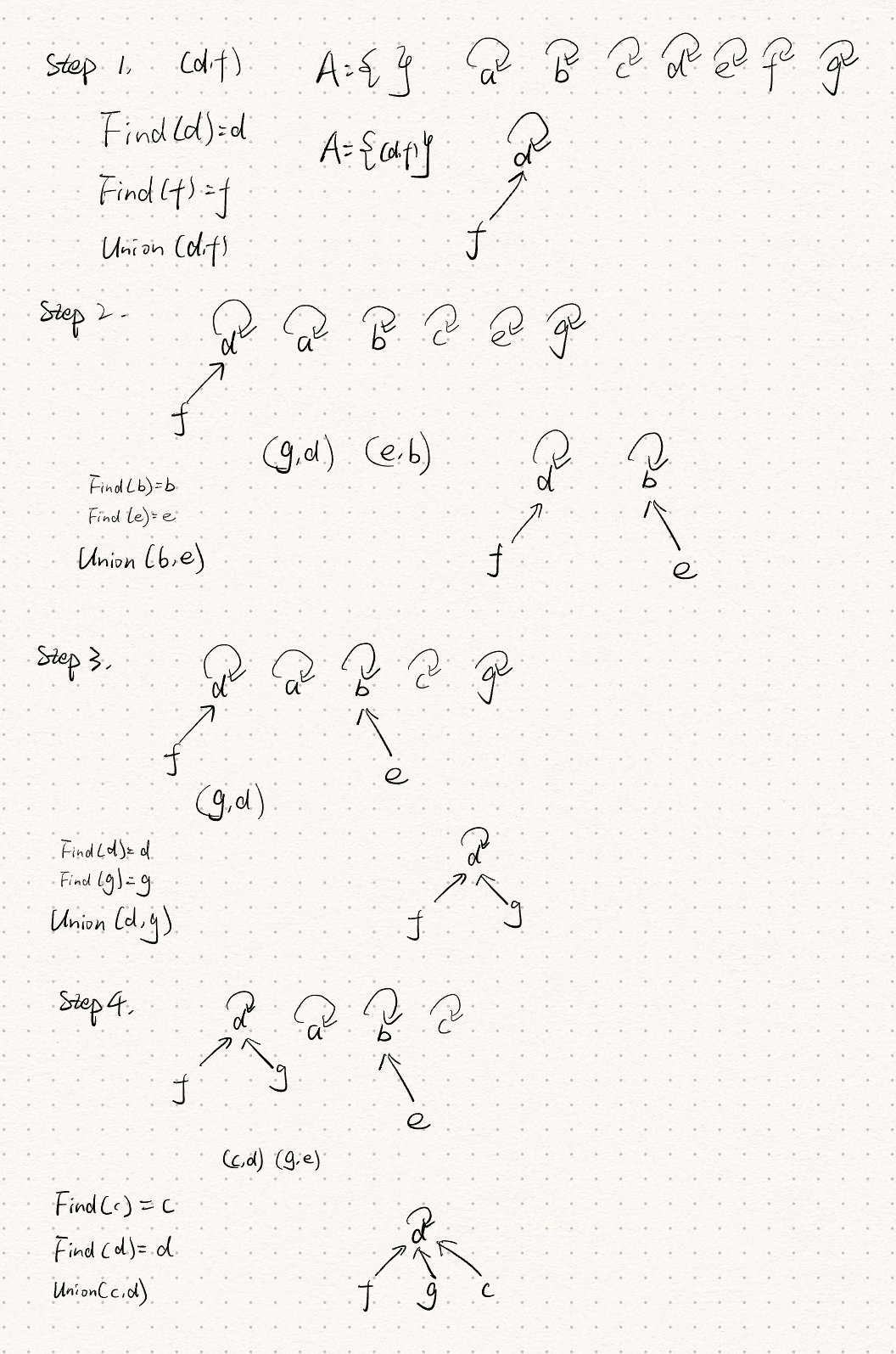
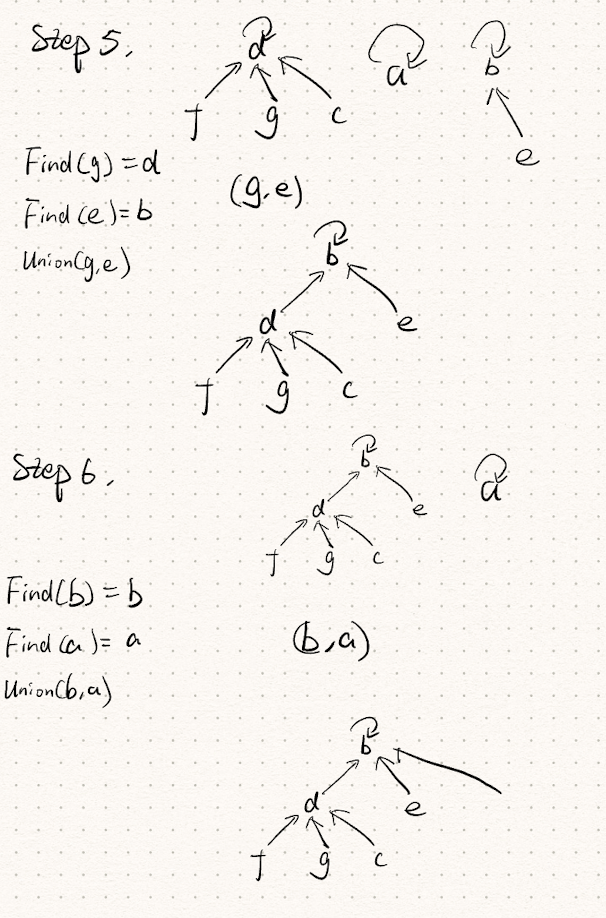
Algorithm MaxST(G, w)

Require: a connected graph $G = (V, E)$ with a weight function $w: E \to \mathbb{Z}$

Ensure: the maximum spanning tree $T$ of $G$

begin

$E \gets \text{sort}(E)$ in decreasing order based on $w$

$A \gets \{\}$

for all $u \in V$ do

$\text{CREATE-SET}(u)$

end for

for all $(u, v) \in E$ do

if $\text{FIND-SET}(u) \neq \text{FIND-SET}(v)$ then

add $(u, v)$ to $A$

$\text{UNION}(u, v)$

end if

end for

return $(V, A)$

end

Note that his algorithm is exactly same as Kruskal’s algorithm except that the loop from line 7 to 12 iterates on edges in the decreasing order. (15pts)

I think his opinion is correct.

Definitions

Heavy Edge: An edge is considered a heavy edge crossing a cut if its weight is the maximum among all edges crossing that cut.
Safe Edge: An edge is considered safe if its inclusion in the growing forest does not violate the properties of the maximum spanning tree (i.e., it does not create a cycle with edges already included in the MST and its addition results in a spanning tree with the maximum possible total weight).

Proof

Case I: Heavy Edge is Safe Edge

If the heavy edge is part of the MST, then by definition, it contributes to forming the maximum possible weight of the MST.
Since it is the heaviest edge across a particular cut and it is part of the MST, it is safe because its exclusion would result in a non-optimal tree (i.e., a tree with less total weight).

Case II: Heavy Edge is Not Safe Edge

Assume for contradiction that there is a heavy edge across a cut which is not included in the MST, implying it is not safe.
If is the heaviest edge crossing the cut and is not included, then to maintain connectivity and maximize total weight, there must be another edge through the cut.
However, was defined as the heaviest edge, so no edge can have a greater weight than.
This leads to a contradiction because it would imply that the current MST is not truly the maximum spanning tree as excluding reduces the possible total weight.

Question 5

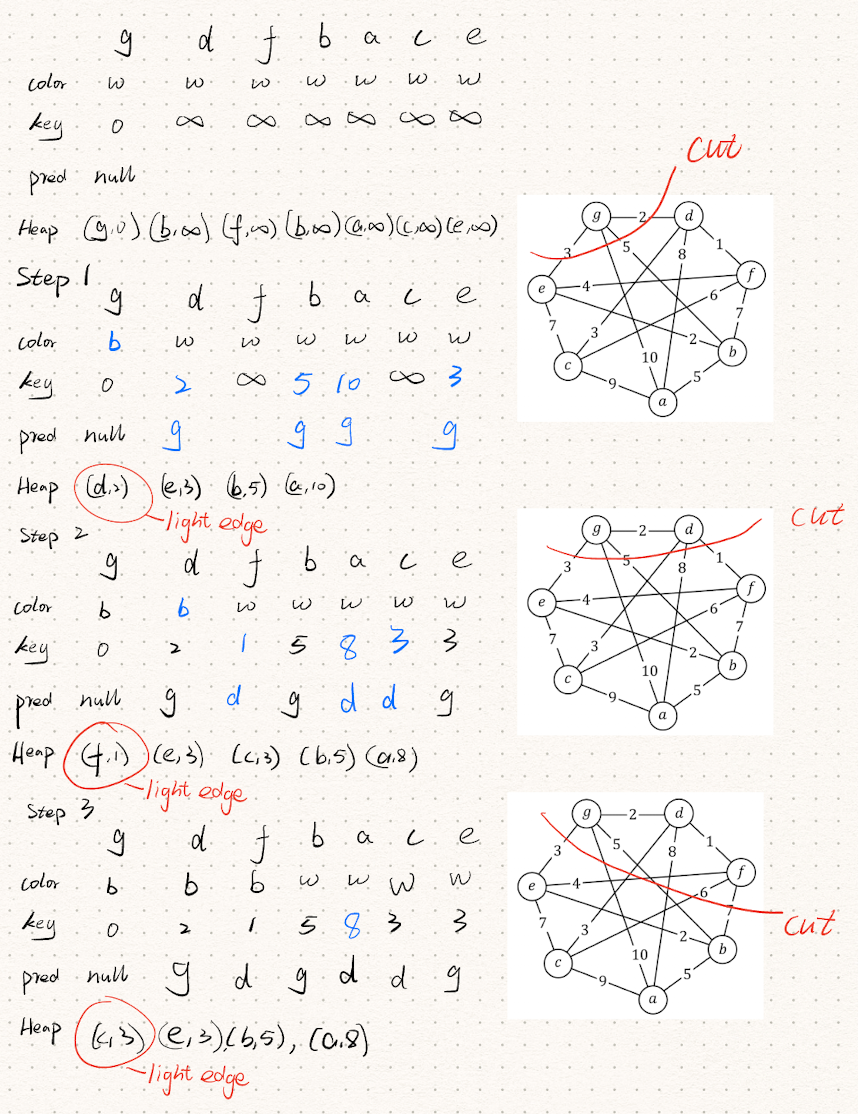
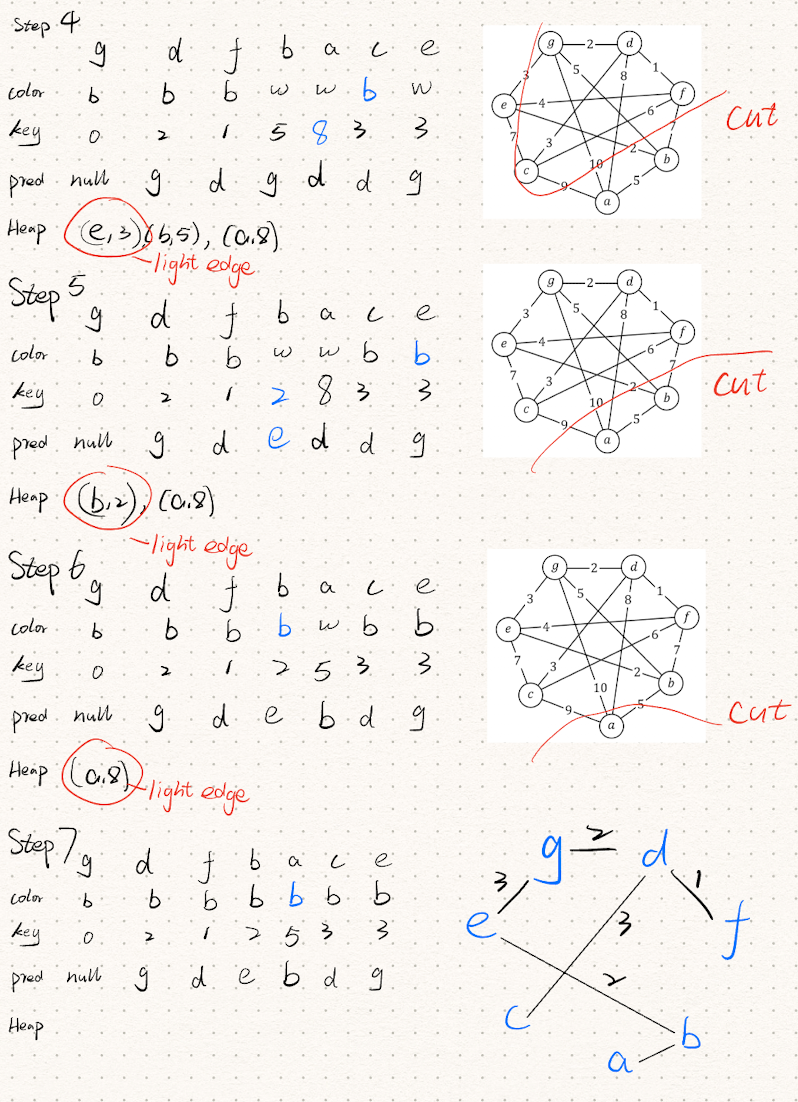
Given a weighted connect graph , a path from to is simple if no vertex on the path is repeated. A simple path is maximum if the length on the simple path is the largest. Such length is called maximum distance from to , denoted as .

Mr. Smart designs the following algorithm to find the maximum simple path from one vertices to all other vertices. Is his algorithm correct? Prove your answer.

Algorithm MaxSP(G, w, s)

Require: a connected graph $G = (V,E)$ with a weight function $w: E \rightarrow \mathbb{Z}$ , a source vertex $s \in V$

Ensure: the maximum distance $\Delta(s,v)$ for all $v \in V$

begin

for all $u \in V$ do

$d[u] \gets \infty$

$color[u] \gets W$

end for

$d[s] \gets 0$

$pred[s] \gets \text{NULL}$

$Q \gets \text{new PriorityQueue}(V)$

while $Q$ is not empty do

$u \gets Q.\text{extractMax}()$

for all $v \in \text{adj}[u]$ do

if $d[u] + w(u,v) > d[v]$ then

$d[v] \gets d[u] + w(u,v)$

$Q.\text{increaseKey}(v, d[v])$

$pred[v] \gets u$

end if

end for

$color[u] \gets B$

end while

return $d[u]$ for each $u \in V$

end

Note that his algorithm is exactly same as Dijkstra’s algorithm except that the priority queue is implemented by a Max Heap. Each round of the loop from line 9 to 19 extract the largest weight edge. And is updated if . (15pts)

I think his algorithm is not correct.

When updating distances using the condition , the algorithm attempts to assign new values based on the assumption that there exists a greater path value from through to.
However, since all are initially , the algorithm's condition will always find that is false, because you cannot have a real number that is greater than . This results in no updates to .

Question 6

From the lecture, Mr. Smart knows that Prim’s algorithm runs in time and Kruskal’s algorithm runs in time. Then, Mr. Smart claims that the time complexity of Prim’s algorithm is lower than Kruskal’s algorithm. Is he correct? Prove your answer. (10pts)

I think he is not correct.

Time Complexities

Prim's Algorithm: Actually as , where is the number of edges, and is the number of vertices.
Kruskal's Algorithm: Commonly has a complexity of .

Dense map

In dense graphs, there are far more edges than vertices, for example .

The time complexity of Prim's algorithm is .
The time complexity of Kruskal's algorithm is .
In this case, the time complexity of Prim's algorithm is lower than Kruskal's algorithm.

Sparse graph

In a sparse graph, the number of edges is close to the number of vertices, that is, .

The time complexity of Kruskal's algorithm is , because the number of edges is small, the sorting burden is relatively light.
The time complexity of Prim's algorithm is .
In this case, the time complexity of Kruskal's algorithm is lower than that of Prim algorithm.

Conclusion

Therefore, it cannot be said that the time complexity of Prim's algorithm is always lower than that of Kruskal's algorithm.