date: 2024-06-22
title: Manacher Algorithm
status: DONE
dg-publish: true
author:
- AllenYGY
tags:
- Manacher
- String
- NOTE
- Algorithm
created: 2024-06-22T00:52
updated: 2024-06-23T16:15Manacher Algorithm
最长回文子串
最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
Brute Force
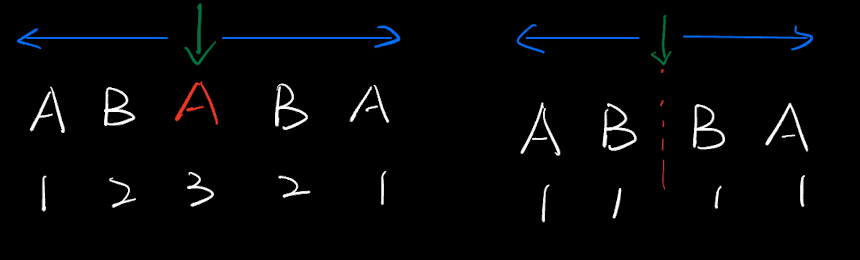
- 对每个字符都向两侧扩展,判断是否为回文串
- 偶数回文串无法直接中心扩展
扩展串
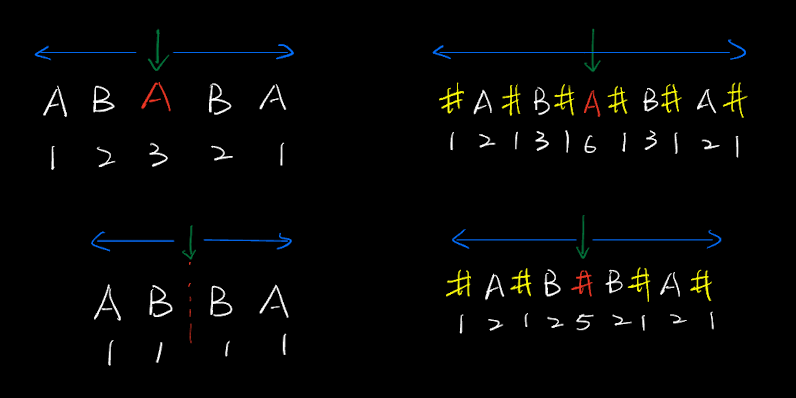
- 在每个字符前后插入一个扩展字符,使字符串长度一定为奇数
- 可以方便的寻找奇长度、偶长度的回文,扩展字符可以随意设置,不会影响计算
Manacher Algorithm
回文覆盖最右边界r、回文中心c
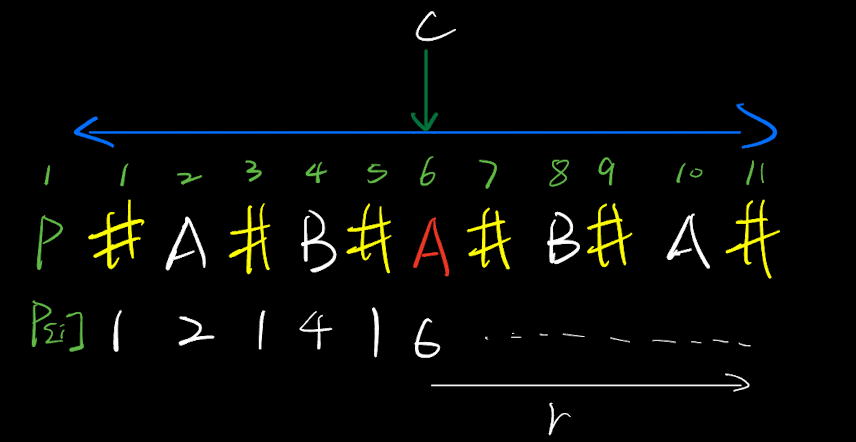
- 在一个大的回文区域内,无需对回文中心之后的每个字符暴力扩展,就可以得到该字符的最大回文半径
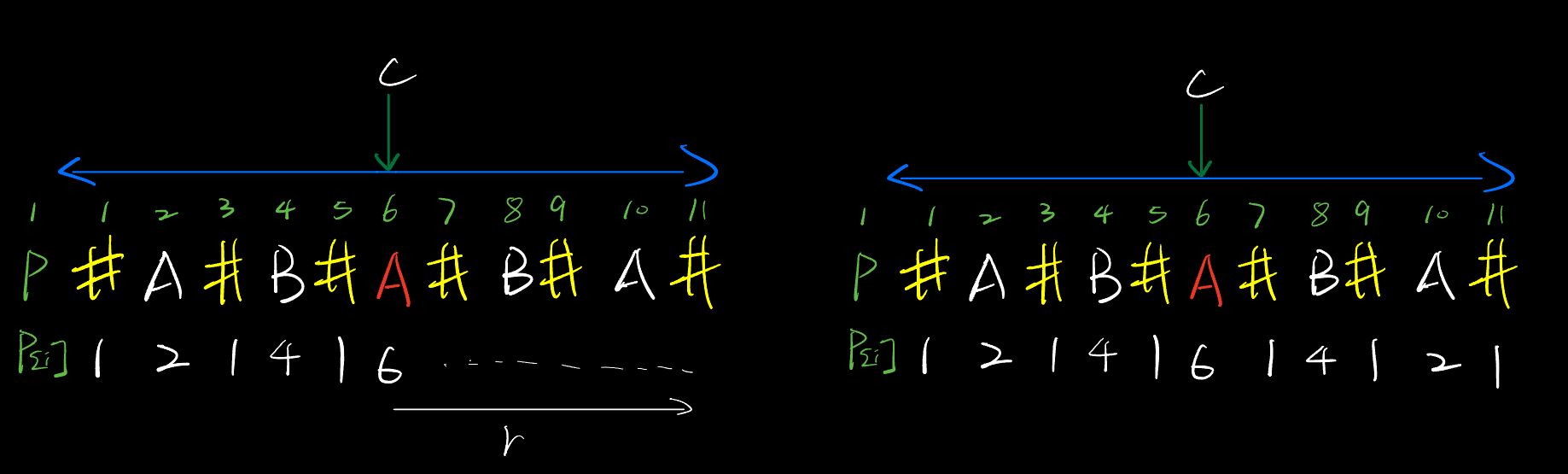
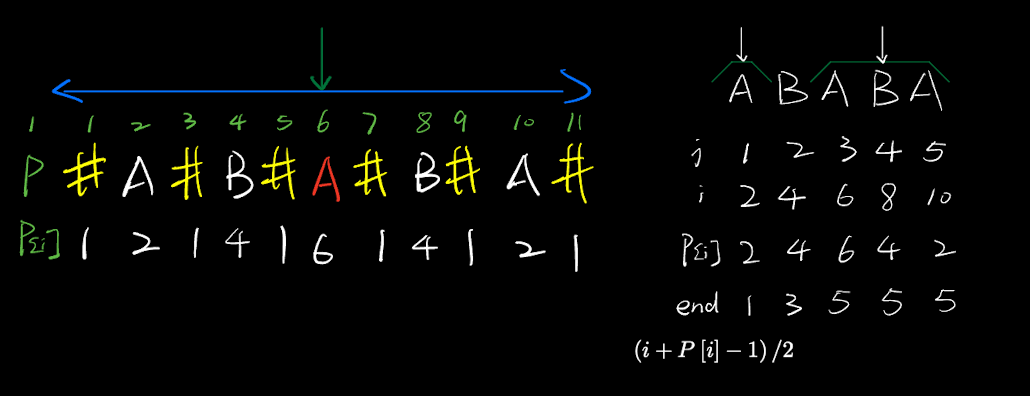
假设一个字符串 s, 字符串s的 Manacher扩展串为 p,p[i] 表示当前字符可以扩展的最长回文串的长度
Manacher算法流程
现在假设我们要对下一个
-
如果
- 以i为中心想两侧扩展,检验字符是否相同,直到不同
-
如果
- 首先计算出对称点的下标
- 当前下标
即
- 当前下标
- 首先计算出对称点的下标
Case 1
- 因为其对称点已经无法扩展,所以其本身也无法扩展
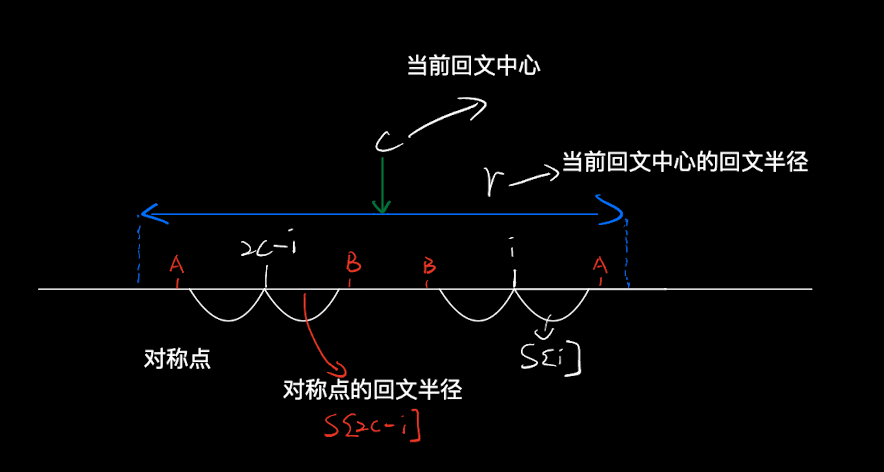
Case 2
2*c-i 的回文半径 s[2*c-i],在大回文区域以外,直接确定
- 因为大回文串已经无法扩展,所以其本身也无法扩展
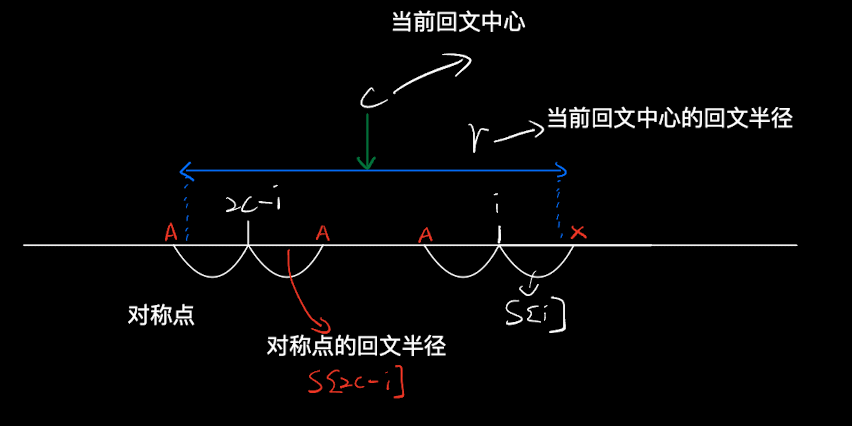
Case 3
- 从r之外的位置进行扩展
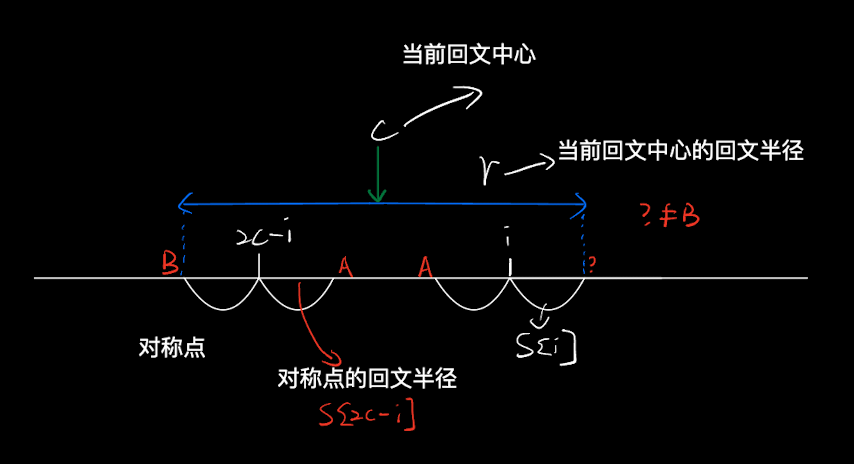
回文半径和实际回文串长度的对应关系
当前字符最长回文串的实际长度
- 每个子字符串扩展后的长度为
- 每个子回文字符串扩展后的回文半径为
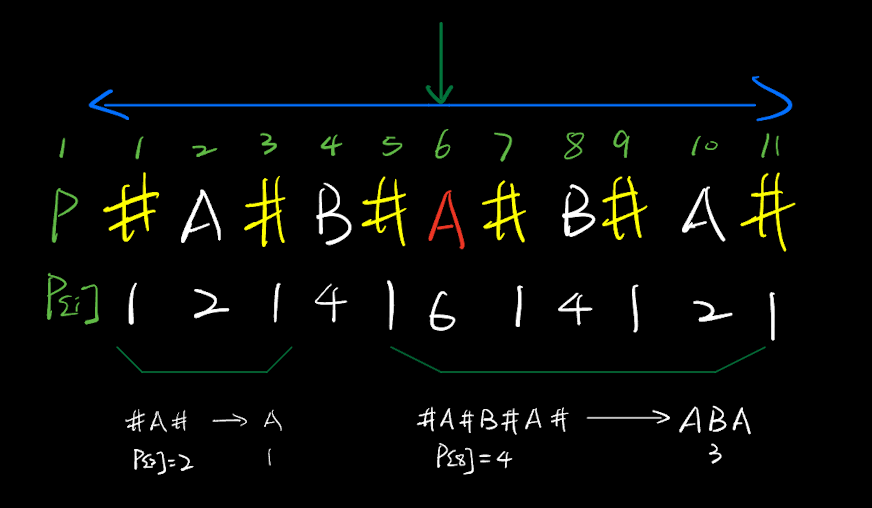
扩展回文串结尾下标和实际回文串终止位置的对应关系
实际回文串终止位置 = 扩展回文串结尾下标 / 2
Manacher CODE
string Preprocess(string s) { // 字符串预处理
string res = "#"; //在每个字符前后添加扩展字符
for (int i = 0; i < s.size(); i++) {
res += s[i];
res += "#";
}
return res;
}
string Manacher(string s) {
string t = Preprocess(s);
string ans = "";
vector<int> p(t.size(), 0);
int mx = 0;
for(int i = 0, c = 0, r = 0, len; i < t.size(); i++) {
// 当 i < r 时,
// 若此时 i + s[i] 在 r 内, 则 r - i >= p[2 * c - i]
// len = p[2 * c - i]
// 若此时 i + s[i] 在 r 外, 则 r - i <= p[2 * c - i]
// len = r - i
// 当 i >= r 时
// 回文字符串即为 i 本身,len = 1
len = i < r ? min(r - i, p[2 * c - i]) : 1;
while (i + len < t.size() && i - len >= 0 && t[i + len] == t[i - len]){ // 不管是否可以扩展,都尝试扩展
len++;
}
if (i + len > r){ //更新新的回文中心和回文半径
r = i + len;
c = i;
}
if(len > mx){ // 维护最长回文子字符串
mx = len;
ans = s.substr((i - len + 1)/2, len - 1);
}
p[i] = len;
}
return ans;
}
相关题目
647. 回文子串
回文子串
返回字符串s的回文子串数量
2472. 不重叠回文子字符串的最大数目
不重叠回文子字符串的最大数目
给定一个字符串str和一个正数k
你可以随意把str切分成多个子串
目的是找到某一种划分方案,有尽可能多的回文子串
并且每个回文子串都要求长度>=k、且彼此没有重合的部分
返回最多能划分出几个这样的回文子串
P1659 拉拉队排练
拉拉队排练
长度前k名的奇数长度回文子串长度乘积
给定一个字符串s和数值k,只关心所有奇数长度的回文子串
返回其中长度前k名的回文子串的长度乘积是多少
如果奇数长度的回文子串个数不够k个,返回-1
P4555 最长双回文串
最长双回文串
最长双回文串长度
输入字符串s,求s的最长双回文子串t的长度
双回文子串就是可以分成两个回文串的字符串
比如"aabb",可以分成"aa"、"bb"