date: 2025-02-23
title: AM-HW-1
status: DONE
author:
  - AllenYGY
tags:
  - NOTE
  - Assignment
  - AAM
publish: true

AM-HW-1

Problem 1.

Brieﬂy describe the problem statements of Eulerian paths, Chinese Postman Problem, Hamiltonian paths, and Traveling Salesman Problem.

Eulerian paths:The Eulerian Path Problem is a fundamental question in graph theory that asks whether it is possible to traverse each edge of a graph exactly once without repetition. Euler's theorem states that for a graph to have such a path, the number of vertices with an odd degree must be exactly 0 or 2.
Chinese Postman Problem: A postman departs from the post office, traverses every street in his assigned area, and then returns to the post office. He may walk along any street multiple times but must choose the shortest possible route.
Hamiltonian paths: The Hamiltonian Path Problem involves determining whether there exists a path in a graph that visits each vertex exactly once.
Traveling Salesman Problem: The Traveling Salesman Problem (TSP) is a classic problem in optimization and theoretical computer science. It seeks to determine the shortest possible route that visits a given set of cities exactly once and returns to the starting city.

Problem 2.

See Chapter 1.pdf. Draw an Eulerian Path:

i. For Figure 15 Graph 2, starting from point A;

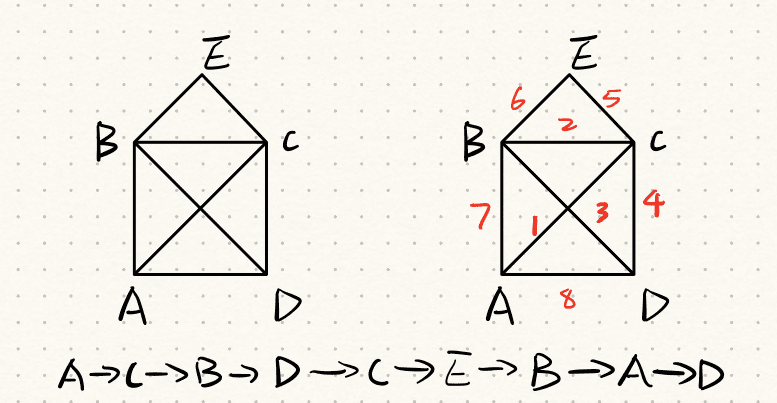
cK8ZDp

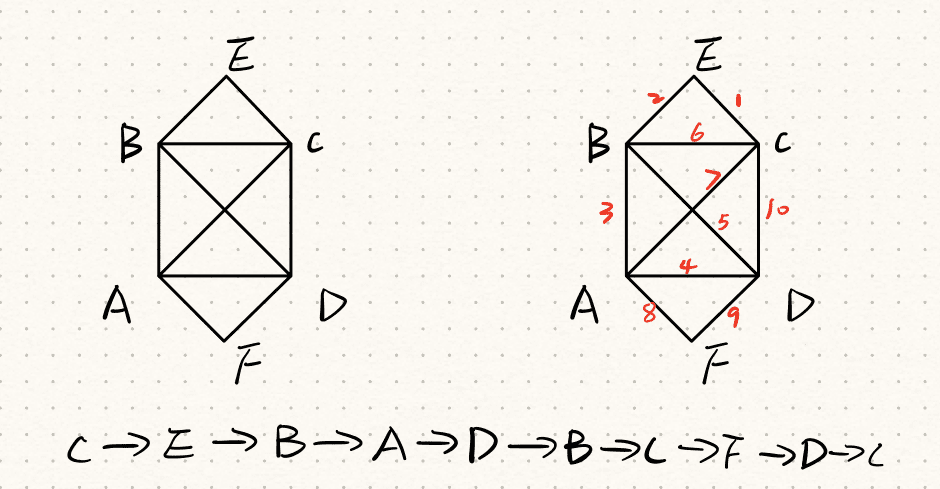
ii. For Figure 15 Graph 3, starting from and ending at point C;

ZFeE7a

iii. Similar to Figure 16, ﬁnd another Chinese character that contains an Eulerian Path.

4q6Qu8

Problem 3.

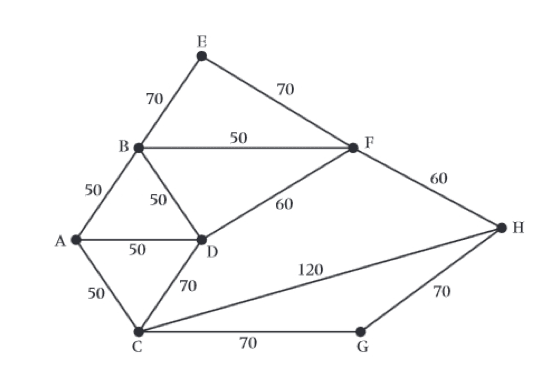
Figure-4

Solve the above Chinese Postman Problem starting and ending at point A by the following steps:

Find all odd vertices, draw their sub-graph with edge weights.

sJYT9F

There are only 2 odd vertices: and . The subgraph with edge weights is 160.

Using the subgraph, ﬁnd which edges to add.

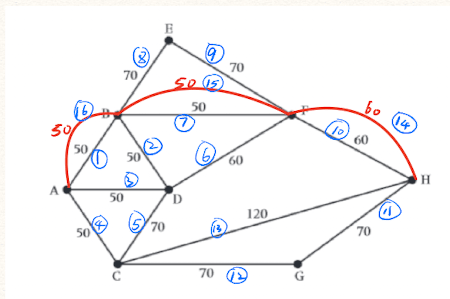
fmy5qK

According to the subgraph, we need to add the following edges to make all vertices even:

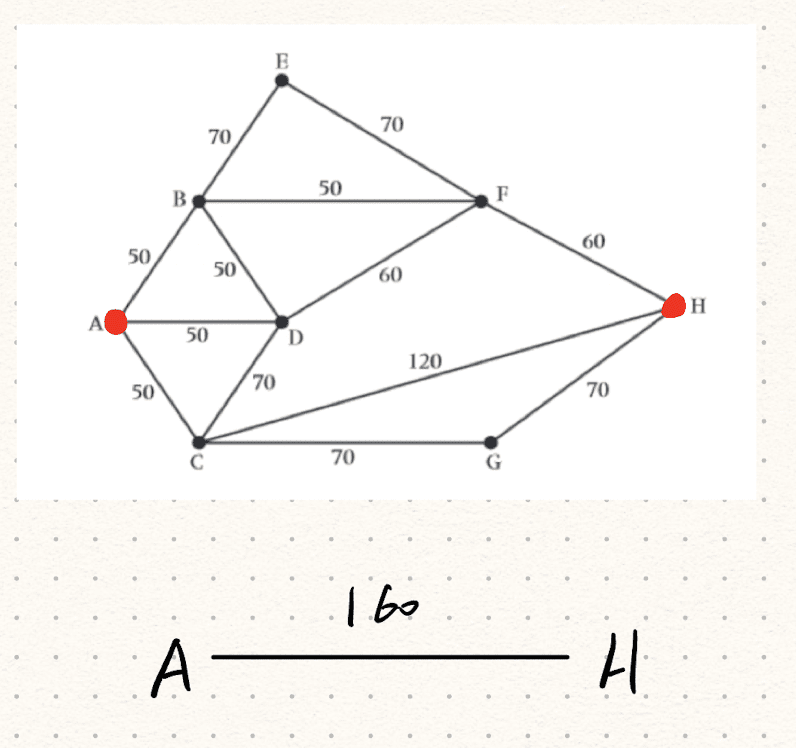
Find the shortest path, and calculate the shortest distance.

fmy5qK

The shortest path which is:
The total length is:

Problem 4.

See Chapter 2.1.pdf.

i. Solve the Traveling Salesman Problem in Figure 2, using brute-force.

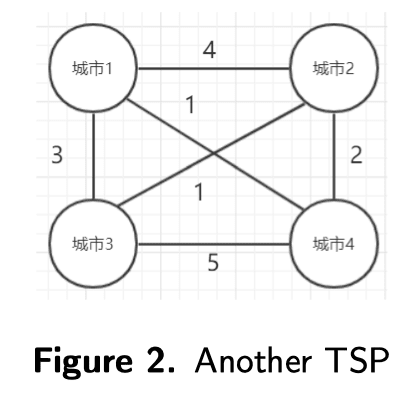
OZ021U

Suppose we start from point 1, and the distance between each pair of points is as follows:

Here are all possible routes, and their total lengths:

So the shortest paths are or , with total distance 7.

ii. Solve the TSP in Figure 1, using branch-and-bound method.

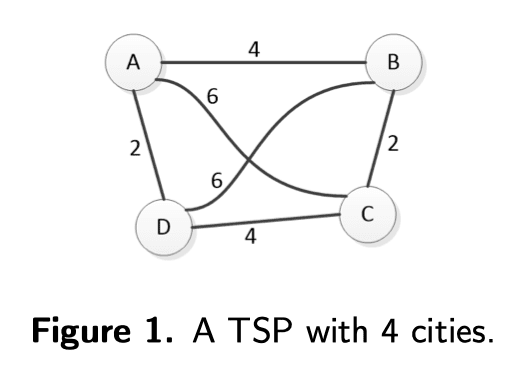
wTyvOc

Suppose the salesman starts and ends at city A with the following distances between each pair of cities:

Path1: ABCDA

Firstly, finish a loop, Path1

The total cost of Path1 = 4+2+4+2=12
Current low cost: 11.

So the lowest cost should be no greater than 12.

Backtrack to the second path.

Path2: ABDC... , cost = 4+6+4=14>12, prune

For the remaining paths, we have:

Path3: ACBD.., cost = 6+2+6=14>12, prune
Path4: ACDB..., cost = 6+4+6=16>12, prune
Path5: ADCBA, cost = 2+4+2+4=12
Path6: ADBCA, cost = 2+6+2+6=16>12, prune

Conclusion:

Shortest paths: ABCDA, ADCBA
Lowest cost: 12

Problem 5.

See Chapter 2.2.pdf.

i. Fill in the cost matrix on page 5.


0	3	6	7
5	0	2	3
3	4	0	2
3	7	5	0

ii. Explain what the sub-problem means in words, and perhaps using a picture or an example.

The sub-problem represents the minimum cost required to start at city , visit all cities in the subset , and return to the home city (usually city 0). Here:

: The current city.
: The set of cities that still need to be visited.

In simpler terms, asks: "What is the minimum cost to finish visiting the remaining cities in , starting from city , and returning to the starting point?"

Simplest Case and Base Condition

Base Case: If , meaning no cities are left to visit, then:
where is the cost of returning directly to the starting city.
Simple Example: If , then:

Example Explanation

Consider a TSP with 4 cities ():

Suppose and .
The sub-problem asks: "What is the minimum cost to start at city , visit both and exactly once (in any order), and then return to the origin city?"

To solve :

The salesman has two options:
- Visit first, then , and return to .
- Visit first, then , and return to .
For each option, the cost is calculated using:
where is the cost of traveling from city to city , and so forth.

iii. With very brief explanations when necessary, solve the TSP using Dynamic Programming by completing the steps on page 6-10.

We consider the following cost matrix , where is the cost of traveling from city to city :

Cost Matrix:

Here, is the starting city, and we aim to find the shortest route visiting all cities and returning to the origin.

Let represent the minimum cost to start at city , visit all cities in subset , and return to the origin. Here's how we solve it step by step:

Step 1: Define Base Case

If (no cities left to visit), the cost is simply the direct cost of returning to the starting city ():

Step 2: Recursive Sub-problem

For each subset of cities and current city , compute using the recursive relationship:
This means the cost of starting at , visiting cities in , and returning to is determined by choosing the next city that minimizes the cost.

Given the provided cost matrix for the Traveling Salesman Problem (TSP), we can solve it step by step using dynamic programming as outlined in the reference material.

Step 3: Solve Sub-problems

Subset

Step 4: Solve for

Finally, solve the original problem :

Compute :

Finally:

The minimum cost for the TSP is 10, The optimal path is .