AAM-HW-4

Problem 1. Currency conversion using slide rule

In 3/26/2025, 1 HKD = 0.934 CNY, 100 JPY = 4.83 CNY.

i.

700 HK dollar is around how many rmb? 85 HKD in RMB? 5100 RMB in HKD?

  • 700 HK dollar is around 653.8 RMB.
  • 85 HKD is around 80.15 RMB.
  • 5100 RMB is around 5460.38 HKD.

ii.

One dish of yakitori at Torikizoku costs 370 yen; how many RMB is that?
Bus ticket from Kansai airport to Osaka station costs 1800 yen; how much is that in RMB?
An anime goods costs 22.5 yuan on Taobao; how much is that converted to yen? (Its local price in Japan is
actually 400 yen.)

  • One dish of yakitori at T orikizoku costs 370 yen is around 17.871 RMB.
  • Bus ticket from Kansai airport to Osak a station costs 1800 yen is around 86.94 RMB.
  • An anime goods costs 22.5 yuan is around 465.838 yen.

Problem 2.

i. How many radians (rad) or degrees (°) is there in one full circle? How many arcminutes (′) are in 1 degree? How many arcseconds (″) are in one arcminute? With this information, you can convert between various angle units: 1 radian equals how many arcseconds? (Write your answer exactly with π, and then approximately as an integer.)

  1. A full circle: or .
  2. 1 degree: .
  3. 1 arcminute: .

Convert 1 radian to arcseconds:

  • Exact value:

  • Approximate value:

ii.

Side question: How many minutes in time does it take for the Sun to move 1 degree or 1 arcminute angle? Every second in time, how many arcminutes or arcseconds does a star rotate in the night sky? [This unfortunate disagreement of factors comes from the 360-degree angle versus 24 hours in one cycle of Earth’s rotation.]

How many minutes (time) does it take for the Sun to move 1 degree or 1 arcminute?

  • The Earth rotates 360° in 24 hours, so:

  • Since 1 degree = 60 arcminutes, the Sun takes:

How many arcminutes or arcseconds does a star rotate every second (time)?

  • The Earth rotates 360° in 24 hours, or:

  • Convert to arcminutes:

  • Convert to arcseconds:

iii.

For an object with diameter whose center is away from the observer, what is the angular diameter (or angular size) , using trigonometry?

If distance is much larger than diameter , approximately what is in radians? In degrees?

T1wmAX

From the geometry of the problem, the angular diameter is the angle subtended by the object at the observer. Using basic trigonometry:

Rearranging:

Thus, the angular diameter is:

Approximation when :

When the distance is much larger than the diameter (), the small-angle approximation applies. In this case:

Using this approximation:

Thus, for small angles:

So, the approximate angular diameter is:

Converting to Degrees:

To convert the angular diameter from radians to degrees:

Thus, the angular diameter in degrees is:

iv.

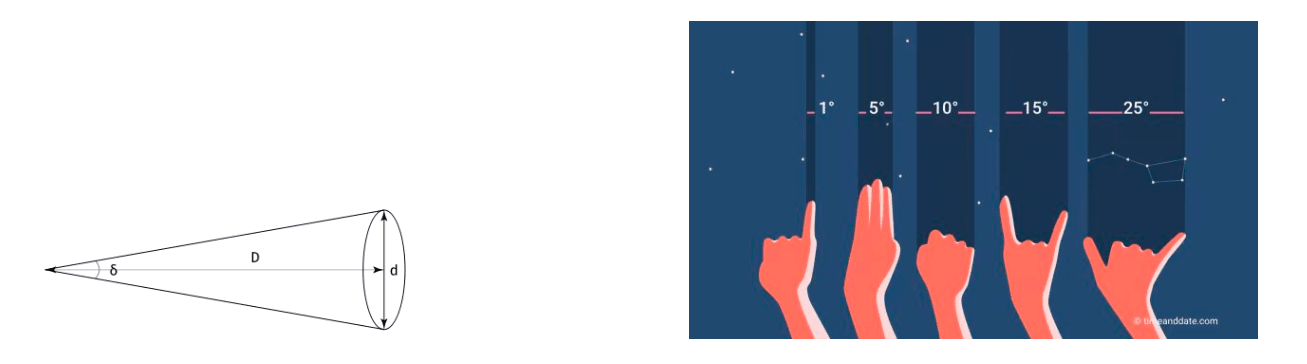
A popular way to estimate angles from your point of view is using parts of you hand, as the diagram above suggests. However these angles might vary from person to person. Use ruler to measure the lengths of the following parts of your hand, and calculate their angular size. Keep 2 or 3 significant digits for measurements and computations. Compare the results from using trigonometry and using small-angle approximation.

Parts Eye-to-palm Pinky Three fingers Fist Pinky-to-Index Pinky-to-Thumb
Length (cm) 60 4 7 10 8 15
Angular size (°) (trigonometry) 3.81 3.81 5.73 9.46 7.63 14.04
Angular size (°) (small-angle approx) 3.81 3.82 6.00 9.00 7.33 14.25

v.

From how far away will your fist appear to have an angular diameter of 1 degree/arcminute/arcsecond?

The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System. It is defined to be the distance D from where Earth-Sun orbit radius appears to be 1 arcsecond apart.

The astronomical unit (symbol: AU) is the average Earth-Sun distance. 1 AU is approximately 1.50 × 1011 meters.

The speed of light in vacuum is approximately 3.00 × 10 meters per second. A light-year (symbol: ly) is the distance that light travels in vacuum in one Julian year (365.25 days). You may take one year to be approximately 365 days.

Compute to 3 significant digits: How many meters is 1 light-year? How many AU is 1 parsec? How many light-years is 1 parsec? In astronomy, it is prefered to use pc, kpc, Mpc, while light-year is used in popular media.]

How many meters is 1 light-year?

First, we need to find the number of seconds in one year:

The speed of light is approximately meters/second. Therefore, the distance light travels in one year (1 light-year) is:

Calculating that gives:

How many AU is 1 parsec?

1 parsec is defined as the distance at which 1 AU subtends an angle of 1 arcsecond. The conversion can be calculated using the formula:

Using the small-angle approximation, where in radians, we convert 1 arcsecond to radians:

Thus, we can rewrite the parsec formula as:

Substituting 1 AU = meters, we get:

To convert parsecs to astronomical units:

How many light-years is 1 parsec?

Using the previously calculated value of 1 parsec in meters:

Now we convert it to light-years:

vi.

By looking up data and doing calculations, verify one object from this comic:

Diameter of Ganymede:

  • The diameter of Ganymede is approximately 5,268 kilometers.

To calculate the estimated area on Earth directly beneath Ganymede:

  1. Radius Calculation:

  2. Area Calculation:
    The area of a circle can be computed using the formula:
    Substituting for :

Comparison with Earth Area

For reference, the surface area of the Earth is about:

Ganymede's area directly beneath it would occupy:

Verification:
The estimated area on Earth's surface directly beneath Ganymede aligns with the general scale referenced in the comic, indicating that Ganymede is a substantial object as represented. Therefore, the depiction of Ganymede in the comic as being equivalent to a large area on the Earth's surface is accurate, based on its size and the calculations performed.

Problem 3. Parts of cosmic distance ladder.

i.

Eratosthenes made the first measurement of the size of Earth. At Syene, southeast of Alexandria in Egypt, the Sun’s rays fall vertically at noon at the summer solstice. Eratosthenes noted that at Alexandria, at the same date and time, sunlight fell at an angle of about from the vertical. He correctly assumed the Sun’s distance to be very great; its rays therefore are practically parallel when they reach Earth. Given an estimate of the distance between the two cities, 5000 stadia, he was able to calculate the circumference of Earth; what is it in stadia? Today we believe that the unit of the "stadium" was about 0.15 km. What is Eratosthenes’s estimate of the Earth’s radius, , in km; what is the percentage error from the currently accepted equatorial radius 6378 km?

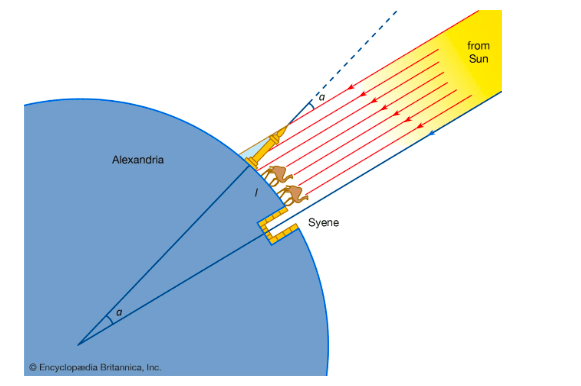
DU62Bi

  1. Angles measured:

    • Angle at Alexandria ():

  2. Distance between the two cities:

    • Distance = stadia.

  3. Conversion factor:

    • stadium km.

Convert Distance to Kilometers

First, we need to convert the distance between the cities from stadia to kilometers:

Calculate the Circumference of the Earth

Eratosthenes used the angle and the distance to calculate the circumference of the Earth. Since the angle at Alexandria is and corresponds to stadia, we can set up a relation to find the total circumference :

The fraction of the circle corresponding to the measured angle is:

So, we can rearrange this to solve for :
Substituting the distance in kilometers:

Calculating this value:

Calculate the Radius of the Earth

The circumference of a circle is related to its radius by the formula:
Rearranging gives:
Substituting in our calculated circumference:

Percentage Error Calculation

Now to determine the percentage error from the currently accepted equatorial radius of the Earth ():

Eratosthenes's estimated radius of the Earth was approximately km, resulting in a percentage error of about 6.32% compared to the currently accepted equatorial radius of km.

ii.

Altair, also known as 牛郎星 in China, has a parallax of mas (milliarcsecond = arcseconds), as measured by Hipparcos satellite. Draw a diagram; how many parsec is Altair from us?

parallax: 0.19444

Earth

Altair

Distance: 5.15 parsecs

iii.

Look up the Hubble constant, especially its units. Cartwheel Galaxy (also known as PGC 2248) has a redshift of km/s from measurement. Estimate its distance.

The Hubble constant () relates the distance of an astronomical object to its redshift (or velocity ) through the formula:

Hubble Constant

The most frequently used value for the Hubble constant is approximately:

Here:

  • is in units of kilometers per second per megaparsec (km/s/Mpc).

Redshift and Distance Calculation

Given the redshift (or velocity) of the Cartwheel Galaxy:

We can rearrange the formula to solve for distance :

Substituting the values we have:

Calculating the distance:

Distance in Other Units

If desired, to convert megaparsecs to light-years (since 1 Mpc ≈ 3.26 million light-years):

The estimated distance to the Cartwheel Galaxy (PGC 2248) is approximately 129.29 Megaparsecs or 421.8 million light-years.

Table Of Contents
AAM-HW-4
Problem 1. Currency conversion using slide rule
i.
ii.
Problem 2.
ii.
iii.
iv.
v.
vi.
Problem 3. Parts of cosmic distance ladder.
i.
ii.
iii.