status: DONE
created: 2024-01-16T21:03
updated: 2024-06-11T01:14
publish: TrueDiscrete Mathematics Assignment-8
Question1
This graph is directed. Because the adjacency matrix is not symmetric
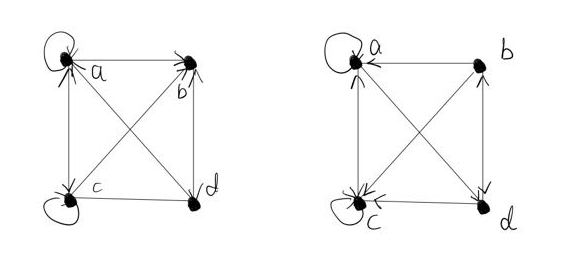
Question2
Question3
- Base Case (n = 1):
For a cube of dimension n = 1, we have 2 vertices connected by an edge. We can easily divide these two vertices into two separate sets, forming a bipartite graph.
For a cube of dimension n = 2, we have 4 vertices connected by an edge. We can easily divide these two vertices into two separate sets like - Inductive Hypothesis:
Assume that a cube - Inductive Step:
Now we need to show that a cube
Next, we assign each vertex in layer L to the opposite set of its connected vertex in
Therefore, we have successfully divided the vertices of - This completes the proof.
Question4
a)
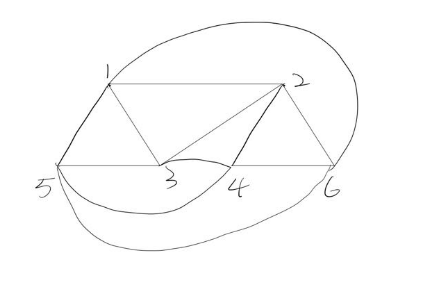
It's clear that the graph is planar. it can be drawn in the plane without any edges crossing
b) It has Euler Circuit cause the thorem A connected multi-graph has an Euler circuit if and
only if each vertex has even degree. The vertex in the graph all has 4 edges. Therefore, it must have Euler Circuit.
c) It has Hamilton Circuits such that 1->2->3 ->4 ->5 ->6->1
Question5
Consider the following graph G = (V, E), where V = {1, 2, 3, 4} and E = {(1, 2), (2, 3), (3, 4), (4, 1), (1, 3)}.
This graph satisfies the condition that for any two non-adjacent vertices u and v in G,
For example, if we take u = 1 and v = 4, then
However, this graph does not have a Hamilton circuit.
Therefore, we have shown that the converse of Ore's theorem is false by providing a counterexample.